Sauter, T., M. Möller, R. Finkelnburg, M. Grabiec, D. Scherer and C. Schneider (2013): Snowdrift modelling for the Vestfonna ice cap, north-eastern Svalbard. – The Cryosphere, 7 (4), 1017-1314. [link]
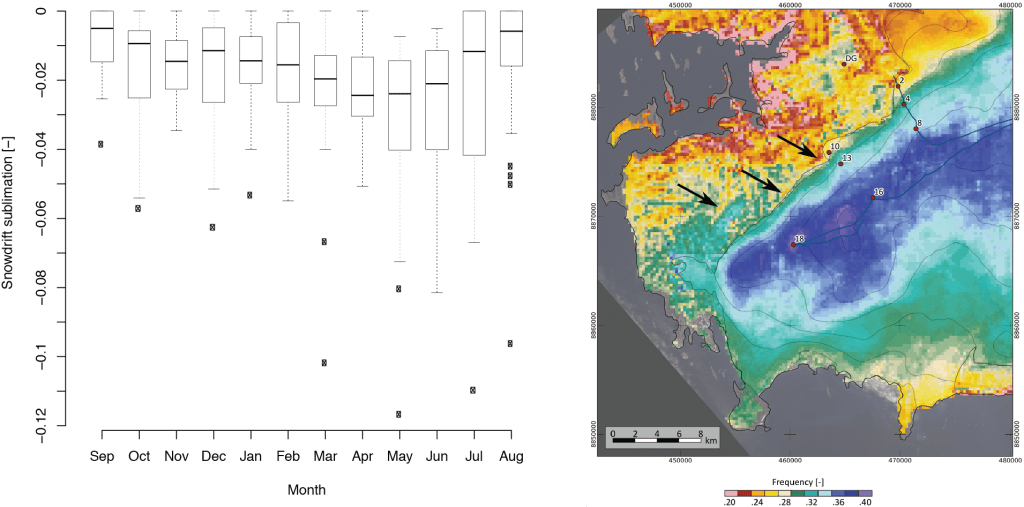
Figure 1: Drifting snow frequency (left) and interseasonal variability (right) of the mean snowdrift sublimation within the near-surface layer (below 10m) for the period September 2008 to May 2009. The drifting snow frequency is defined as the ratio of days with non-zero erosion flux and the total number of days. The locations of snow-pit measurements are denoted as red dots. The blue line shows the radio-echo sounding profile of Grabiec et al. (2011) in May 2009. In the interseasonal variability plot the boxes spread between lower and up- per quartiles of the values with the median shown as the thick line in between, the whiskers extend the boxes by 1.5 times the interquartile range. Values outside this range are considered as outliers.
Assessing the uncertainty of glacier mass balance simulations by decomposing the model variance
State of the art numerical snowpack models essentially rely on observational data for initialization, forcing, parametrization and validation. Such data are available in increasing amount, but the propagation of related uncertainties on the simulation results has received rather limited attention so far. Depending on their complexity, even small errors can have a profound effect on simulations, which dilutes our confidence in the results. This paper aims at quantification of the overall and fractional contributions of some archetypical measurement uncertainties on snowpack simulations in Arctic environments.
Sauter, T. and F. Obleitner (2015): Assessing the uncertainty of glacier mass-balance simulations in the European Arctic based on variance decomposition. – Geosci. Model Dev., 8, 3911-3928, 2015, doi:10.5194/gmd-8-3911-2015. [link]
Figure 1: The map shows the location of Kongsvegen glacier and the position of the automatic weather stations KNG8, KNG6 and KNG1 (Norwegian Polar Institute, 2014).
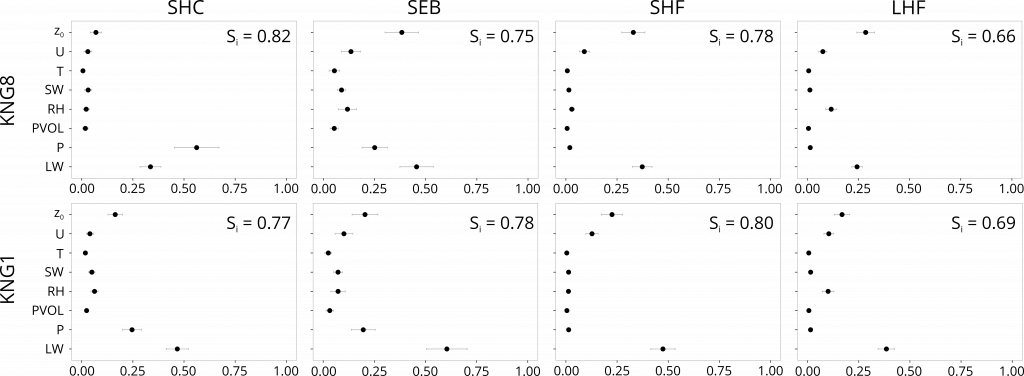
The sensitivity pattern is studied at two sites representing the accumulation and ablation area of Kongsvegen glacier (Svalbard) using the snowpack scheme Crocus. The contribution of measurement errors on model output variance, either alone or by interaction, is decomposed using Global Sensitivity Analysis. This allows investigation of the temporal evolution of the fractional contribution of different factors on key model output metrics, which provides a more detailed understanding of the model’s sensitivity pattern. The analysis demonstrates that the specified uncertainties in precipitation and longwave radiation forcings had an outstanding influence on the calculated surface height changes and surface energy balance components. The model output sensitivity patterns also reveal some characteristic seasonal imprints. For example, uncertainties in longwave radiation trace on calculated surface energy balance rather continuous throughout the year and at both study sites, while precipitation exerts most influence during winter and at the upper site. Such findings are valuable to identify critical parameters and improve their measurement and correspondingly updated simulations may shed new light on the confidence of results from snow or glacier mass and energy balance models. This matters for many applications in the fields of e.g. avalanche and hydrological forecasting.
Figure 2: Yearly averaged total-order effects (on model uncertainty) of factors on surface height change (SHC), surface energy balance (SEB), sensible heat and latent heat flux (HF) at KNG8 and KNG1. The whiskers show the 95% confidence interval derived from 1000 empirical bootstrap samples. The mean (taken over the whole period) of the 6 hourly first-order sums (linear effects) are given in the upper right corner.